Largest Rectangle In Histogram

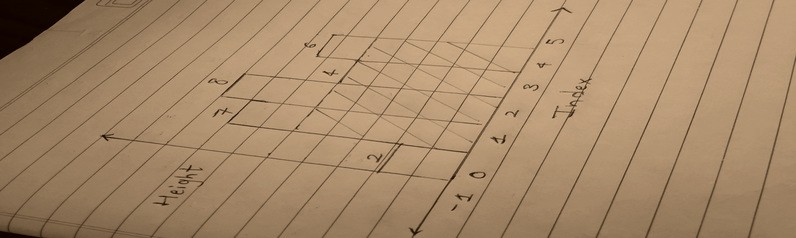
Hey there! This is my first technical post. I’ll be discussing the “Largest Rectangle in Histogram” problem. This problem used to trouble me a lot. But it is an interesting one!

Introduction

You can try it out on your own on binarysearch.com: Problem Link

Example:

If you are given the array : arr = [2, 7, 8, 4, 6], the histogram will look like this.

Clearly, the solution to the problem will be the shaded rectangle.

We will use this input as an example throughout the post.

Naive Solution

On careful observation, we can notice that the height of the largest rectangle will always be the height of one of the bars present in the input array. This actually helps us to develop a naive solution.

Here is a C++ implementation for the same:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int solve(vector<int>& arr) {
    int n = arr.size(), max_area = 0, lo, hi, width, height;

    for (int i = 0; i < n; i++) {
        height = arr[i];
        lo = hi = i;
        while (lo >= 0 && arr[lo] >= height) lo--; // expand bar to left
        while (hi < n && arr[hi] >= height) hi++;  // expand bar to right
        width = hi - lo - 1;                       // calculate width
        max_area = max(max_area, width * height);  // update global ans
    }
    return max_area;
}

The time complexity of this code is $O(n^{2})$ which is too slow.

A Better Solution

• In the Naive approach, we essentially try to extend a bar to the left and right directions until we come across a bar which is smaller than it. So in essence, we only care about the location of the first bar which is smaller to the left and the first bar which is smaller to the right. Now, what if we had a way to precompute the locations of the next smaller bar for every bar, for both its left and right side? This will allow us to get rid of the two inner while loops.

• It turns out that you can perform this precomputation in $O(n)$ time using stack. This is actually a variant of the classic Next Greater to the Right (NGR) problem. In this case, we are concerned with the location of the next smaller elements. The NGR problem can be solved using monostack.

• You are expected to return an vector/array of size $n$ such that : ans[i] = Index of the next smaller element(bar) to the left of arr[i]

• For our convenience, we assume that there is an imaginary zero height bar at index -1 as shown in the below figure. Consequently, for a bar $b_{i}$ which has no smaller bar to its left, we set ans[i] = -1, indicating that the imaginary zero height bar is the next smaller to its left. This explains the initialization of the ans vector to -1 when its declared. We make a similar assumption for the Nearest Smaller to the Right (NSR) problem. In NSR, the imaginary zero height bar is at index n.

• The solution for Next Smaller to the Left ( NSL ) problem for the histogram in our example can be given as: ans[i] = [-1, 0, 1, 0, 3]. The figure below gives more insight on how we obtain the solution. The arrows point to the next smaller bar to the left for every bar.

• Similarly we can build an answer for Next Smaller to the Right ( NSR ) problem. ans[i] = [5, 3, 3, 5, 5 ].

Here’s an implementation for Nearest Smaller to the left ( NSL ) problem.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

vector<int> NSL(vector<int>& arr) {
    /*
    Returns a vector as a solution for Nearest Smaller to the Left Problem
    */
    int n = arr.size();
    stack<int> stk;

    vector<int> ans(n, -1);
    for (int i = 0; i < n; i++){
        while (!stk.empty() && arr[stk.top()] >= arr[i]){
            stk.pop();
        }
        if (!stk.empty()) ans[i] = stk.top();
        stk.push(i);
    }
    return ans;
}

Implementation for NSR:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

vector<int> NSR(vector<int>& arr){
    /*
    Returns a vector as a solution for Nearest Smaller to the Right Problem
    */
   int n = arr.size();
    stack<int> stk;
    vector<int> ans(n, n);

    for (int i = n - 1; i >= 0; i--){
        while (!stk.empty() && arr[stk.top()] >= arr[i]) {
            stk.pop();
        }
        if (!stk.empty()) ans[i] = stk.top();
        stk.push(i);
    }
    return ans;
}

Putting it all together:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int solve(vector<int>& arr) {
    int n = arr.size(), max_area = 0, lo, hi, width, height;
    vector<int> left = NSL(arr);
    vector<int> right = NSR(arr);

    for (int i = 0; i < n; i++) {
        height = arr[i];
        lo = left[i], hi = right[i];
        width = hi - lo - 1;
        max_area = max(max_area, width * height);
    }
    return max_area;
}

Notice how we got rid of the two inner while loops in the naive approach!

Time Complexity of this approach is $O(n)$.

Space Complexity is $O(2n)$ as we are using two arrays, left and right for storing NSL and NSR.

Can we do better ???

An Elegant Solution!

• It is possible to solve this problem in a single pass using monostack, very similar to the way we solve the Next Greater to the Right (NGR) problem.

• We push elements (bar heights) into the monostack in a strictly increasing order as we move form left to right. This is an invariant that we always maintain. Since, we care about the location of the elements, we push their indices instead of the values. We can always access the values as per our needs when we have the indices.

• In the following section, I’ll be referring to the indices of bar heights as bar heights themselves.

• If the current bar height $b_i$ is greater than the bar height on the top of the stack (or if the stack is empty ), then we simply push the index $i$ on the top of the stack and move on.

• In our example, arr = [2, 7, 8, 4, 6] the array is strictly increasing till index 2. So, we simply add the indices into the stack sequentially.

• But when we encounter a bar height $b_i$ which is shorter than the bar height on the top of the stack, say $b_j$ ( $b_j < b_i$ and $j < i$ ), we can conclude that $b_j$ cannot be expanded beyond index $i$ towards the right.

• In our example, when $i = 3$, $b_i = 4$. The bar height of the index on top of the stack $j = 2$ is $b_j = 8$. So here, $b_j > b_i$ as $8 > 4$. We now come to know that the bar height $b_j$ = 8 cannot be expanded further as $b_i = 4$ is not big enough to expand $b_j$’s rectangle.

• Since $b_j$ was present in the stack so far, we know for sure that $b_j$ can be expanded uptil index $i-1$. It remains to find out how much it it can be expanded to the left.

• In our example, for $b_j = 8$, we know that $b_j$ can be expanded only uptil index $i - 1$ i.e $3-1 = 2$. This is our rightmost expansion point for $b_j = 8$.

• To find the left expansion point, we can make use of of the fact that the stack is strictly increasing! Our left expansion point is simply the index of the bar $b_k$ in the stack, below the top element $b_j$. This is because it is guaranteed that $b_k$ < $b_j$ (also $k < j$) and hence, $b_j$ can only be expanded uptil index $k+1$ to the left. If $b_k$ does not exist, then the stack will be empty. However, we can assume $k$ as $-1$ in this case for mathematical convenience.

• In our example, for $b_j = 8$ the index $k$ is $k = 1$ as $b_k = 7$ and $b_k < b_j$. So the left expansion point for the bar height $8$ is $k + 1 = 2$.

• At its core, the solution is simply a more elegant version of the second approach we saw earlier. $b_k$ is the next smaller element to the left of $b_j$ and $b_i$ is the next smaller element to the right of $b_j$.

• So bar height $b_j$ spans from $k+1,k+2,…j,…,i-1$. The width of the rectangle it forms is $i - k - 1$. ( Note that $k < j < i$ ). So the height of the rectangle is $b_j$ and its width is $i - k - 1$. Using them, we update our global maximum answer. After all this, we can say that we have completely processed element $b_j$. We pop index $j$ out of the stack.

• We keep on popping out bar heights from the top of the stack until $b_i$ is smaller or equal to the bar height on the top of the stack. Once, we have processed all the bar heights from the stack we push index $i$ onto the stack with the hope of $b_i$ getting expanded further to the right.

• If the stack is non-empty at the end, we process the remaining elements in the stack with the same algorithm, assuming we have a zero height bar at index $n$ as mentioned earlier ( We assume $i = n$).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

int solve(vector<int>& nums) {
    int n = nums.size();
    stack<int> stk;
    int max_area = 0 , cur_area , height , k , width;

    for(int i = 0; i < n ; i++){
        while(!stk.empty() && nums[stk.top()] >= nums[i]){
            height = nums[stk.top()];  // This height is bj
            stk.pop();
            k = stk.empty() ? -1 : stk.top();
            width = i - k - 1;
            cur_area = height * width;
            max_area = max(cur_area , max_area);
        }

        stk.push(i); // Pushing index i onto the stack after processing elements from stack.
    }

    // We process the remaining elements in the stack.
    while(!stk.empty()){
        height = nums[stk.top()];   // This height is bj
        stk.pop();
        k = stk.empty() ? -1 : stk.top();
        width = n - k - 1;          // In this case, i = n
        cur_area = height * width;
        max_area = max(cur_area , max_area);
    }

    return max_area;
}